他鼓起足够的勇气,在董事会会议上打破僵局。
He got up enough guts to breakthe ice at the board meeting.
网校学员Poi**在学习《大学英语六级全程备考班【小橙卡专享班】》时提出了此疑惑,已有4人帮助了TA。

网校助教
czs3634
同学你好,该知识点来自沪江网校《大学英语六级全程备考班【小橙卡专享班】》的课程,想要更系统的学习,欢迎进入课程学习。不仅可以和更多的同学一起学习,而且还有老师、助教随时的学习指导和知识点解答哦。
∵cos^4xsin^2x=cos^4x(1-cos²x)
=cos^4x-cos^6x
=[1+cos(2x)]²/4-[1+cos(2x)]³/8
=[1+2cos(2x)+cos²(2x)]/4-[1+3cos(2x)+3cos²(2x)+cos³(2x)]/8
=1/8+1/8cos(2x)-1/8cos²(2x)-1/8cos³(2x)
=1/8+1/8cos(2x)-[1+cos(4x)]/16-1/8cos³(2x)
=1/16+1/8cos(2x)-cos(4x)/16-1/8cos³(2x)
∴∫cos^4xsin^2xdx
=∫[1/16+1/8cos(2x)-cos(4x)/16-1/8cos³(2x)]dx
=x/16+sin(2x)/16-sin(4x)/64-1/16∫[1-sin²(2x)]d[sin(2x)]
=x/16+sin(2x)/16-sin(4x)/64-[sin(2x)-sin³(2x)/3]/16+C
=x/16-sin(4x)/64+sin³(2x)/48+C
刚才那张图有点问题

网校助教
czs3634
同学你好,该知识点来自沪江网校《大学英语六级全程备考班【小橙卡专享班】》的课程,想要更系统的学习,欢迎进入课程学习。不仅可以和更多的同学一起学习,而且还有老师、助教随时的学习指导和知识点解答哦。
∵cos^4xsin^2x=cos^4x(1-cos²x)
=cos^4x-cos^6x
=[1+cos(2x)]²/4-[1+cos(2x)]³/8
=[1+2cos(2x)+cos²(2x)]/4-[1+3cos(2x)+3cos²(2x)+cos³(2x)]/8
=1/8+1/8cos(2x)-1/8cos²(2x)-1/8cos³(2x)
=1/8+1/8cos(2x)-[1+cos(4x)]/16-1/8cos³(2x)
=1/16+1/8cos(2x)-cos(4x)/16-1/8cos³(2x)
∴∫cos^4xsin^2xdx
=∫[1/16+1/8cos(2x)-cos(4x)/16-1/8cos³(2x)]dx
=x/16+sin(2x)/16-sin(4x)/64-1/16∫[1-sin²(2x)]d[sin(2x)]
=x/16+sin(2x)/16-sin(4x)/64-[sin(2x)-sin³(2x)/3]/16+C
=x/16-sin(4x)/64+sin³(2x)/48+C
刚才那张图有点问题

网校助教
czs3634
同学你好,该知识点来自沪江网校《大学英语六级全程备考班【小橙卡专享班】》的课程,想要更系统的学习,欢迎进入课程学习。不仅可以和更多的同学一起学习,而且还有老师、助教随时的学习指导和知识点解答哦。
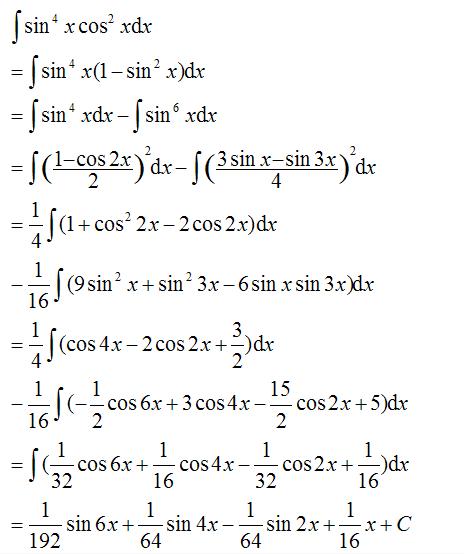
刚才那个助教给你的是递推的式子,4次你递推,推完了考试也结束了。这种题目太偏了,没事不要研究它

网校助教
czs3634
同学你好,该知识点来自沪江网校《大学英语六级全程备考班【小橙卡专享班】》的课程,想要更系统的学习,欢迎进入课程学习。不仅可以和更多的同学一起学习,而且还有老师、助教随时的学习指导和知识点解答哦。
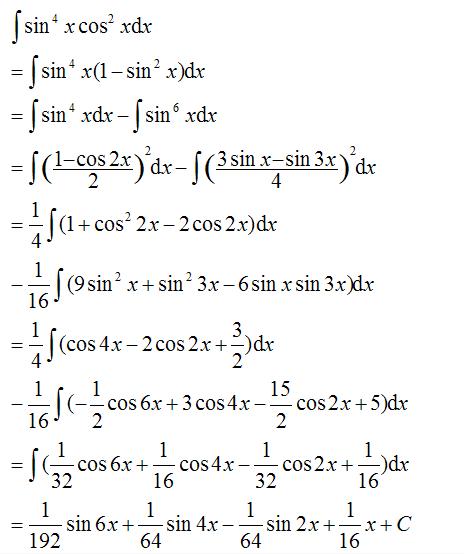
刚才那个助教给你的是递推的式子,4次你递推,推完了考试也结束了。这种题目太偏了,没事不要研究它
版权申明:知识和讨论来自课程:《大学英语六级全程备考班【小橙卡专享班】》的学员和老师,如果想了解更多,可以报名参加课程学习。所有知识讨论内容,版权归作者及沪江网校所有。
以上知识点和讨论均来自沪江网校,点击了解课程详情
